Find Gof A B Discrete Mathematics Solution Exam Pdf

Functions are relations where each input has a particular output. In this lesson, the concepts of functions in mathematics and the different types of functions are covered using various examples for better understanding.

Contents Related to Functions

Functions
Limits, Continuity and Differentiability
Differentiation
Applications of Derivatives

JEE Main 2021 Maths LIVE Paper Solutions 24-Feb Shift-1 Memory-Based

What are Functions in Mathematics?

A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets, mapping from A to B will be a function only when every element in set A has one end only one image in set B.

Example:

Functions

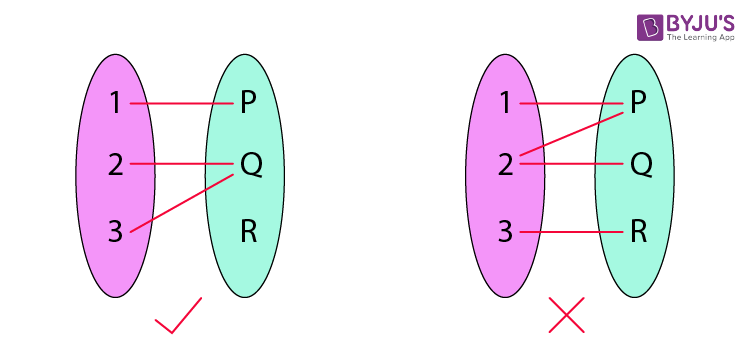
Another definition of functions is that it is a relation "f" in which each element of set "A" is mapped with only one element belonging to set "B". Also in a function, there can't be two pairs with the same first element.

A Condition for a Function:

Set A and Set B should be non-empty.

In a function, a particular input is given to get a particular output. So, A function f: A->B denotes that f is a function from A to B, where A is a domain and B is a co-domain.

For an element, a, which belongs to A, $a\epsilon A$ , a unique element b, $b\epsilon B$ is there such that (a,b) $\epsilon$ f.

The unique element b to which f relates a, is denoted by f(a) and is called f of a, or the value of f at a, or the image of a under f.

The range of f(image of a under f)
It is the set of all values of f(x) taken together.
Range of f = { y $\epsilon$ Y | y = f (x), for some x in X}

A real-valued function has either P or any one of its subsets as its range. Further, if its domain is also either P or a subset of P, it is called a real function.

Vertical Line Test:

Vertical line test is used to determine whether a curve is a function or not. If any curve cuts a vertical line at more than one points then the curve is not a function.

Vertical Line Test

Representation of Functions

Functions are generally represented as $f(x)$

Let , $f(x)= x^{3}$

It is said as f of x is equal to x cube.

Functions can also be represented by g(), t(),… etc.

Steps for Solving Functions

Question: Find the output of the function $g(t)= 6t^{2}+5$ at

(i) t = 0

(ii) t = 2

Solution:

The given function is $g(t)= 6t^{2}+5$

(i) At t = 0, $g(0)= 6(0)^{2}+5$

= 5

(ii) At t = 2, $g(2)= 6(2)^{2}+5$

= 29

Types of Functions

There are various types of functions in mathematics which are explained below in detail. The different function types covered here are:

One – one function (Injective function)
Many – one function
Onto – function (Surjective Function)
Into – function
Polynomial function
Linear Function
Identical Function
Quadratic Function
Rational Function
Algebraic Functions
Cubic Function
Modulus Function
Signum Function
Greatest Integer Function
Fractional Part Function
Even and Odd Function
Periodic Function
Composite Function
Constant Function
Identity Function

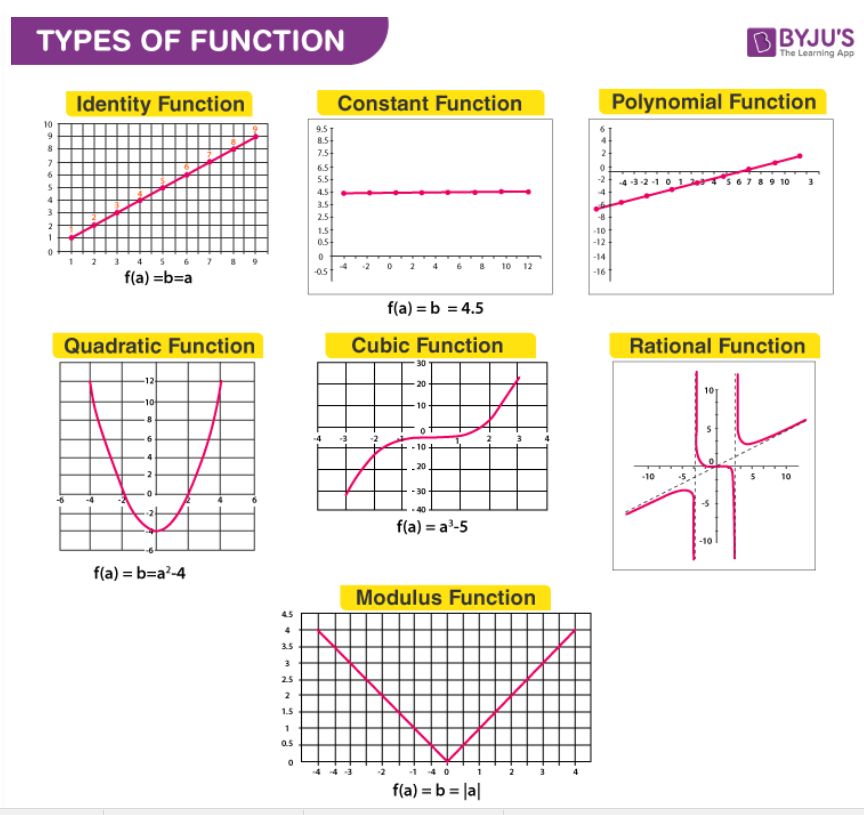
Types of Function

Practice: Find the missing equations from the above graphs.

Number of Functions

One – one function (Injective function)

If each element in the domain of a function has a distinct image in the co-domain, the function is said to be one – one function.

One-to-One Function

For examples f; R R given by f(x) = 3x + 5 is one – one.

Many – one function

On the other hand, if there are at least two elements in the domain whose images are same, the function is known as many to one.

Many-to-One Function

For example f : R R given by f(x) = x² + 1 is many one.

Onto – function (Surjective Function)

A function is called an onto function if each element in the co-domain has at least one pre – image in the domain.

Into – function

If there exists at least one element in the co-domain which is not an image of any element in the domain then the function will be Into function.

(Q) Let A = {x : 1 < x < 1} = B be a mapping f : A B, find the nature of the given function (P). F(x) = |x|

Into – function f (x) = |1|

Solution for x = 1 & -1

Hence it is many one the Range of f(x) from [-1, 1] is

[0,1] which is not equal to co-domain. Hence it is into function.

Into – function Example

Lets say we have function,

f(x)=\left\{\begin{matrix} x^2 & ; & x\geq 0\\ -x^2 & ; & x<0 \end{matrix}\right.

For different values of Input, we have different output hence it is one – one function also it manage is equal to its co-domain hence it is onto also.

Polynomial function

A real valued function f : P → P defined by y = f (a)= $h_{0}+h_{1}a+…..+h_{n}a^{n}$ , where n $\epsilon$ N, and $h_{0}+h_{1}+…..+h_{n}$ $\epsilon$ P, for each a $\epsilon$ P, is called polynomial function.

N = a non-negative integer.
The degree of Polynomial function is the highest power in the expression.
If the degree is zero, it's called a constant function.
If the degree is one, it's called a linear function. Example: b = a+1.
Graph type: Always a straight line.

So, a polynomial function can be expressed as :

$f(x)= a_{n}x^{n}+a_{n-1}x^{n-1}+…..+a_{1}x^{1}+a_{0}$

The highest power in the expression is known as the degree of the polynomial function. The different types of polynomial functions based on the degree are:

The polynomial function is called a Constant function if the degree is zero.
The polynomial function is called a Linear if the degree is one.
The polynomial function is Quadratic if the degree is two.
The polynomial function is Cubic if the degree is three.

Linear Function

All functions in the form of ax + b where a, $b\in R$ & a ≠ 0 are called as linear functions. The graph will be a straight line. In other words, a linear polynomial function is a first-degree polynomial where the input needs to be multiplied by m and added to c. It can be expressed by f(x) = mx + c.

For example, f(x) = 2x + 1 at x = 1

f(1) = 2.1 + 1 = 3

f(1) = 3

Linear Function

Another example of linear function is y = x + 3

Linear Function Example

Identical Function

Two functions f and g are said to be identical if

(a) The domain of f = domain of g

(b) The range of f = the Range of g

(c) $f\left( x \right)\text{ }=\text{ }g\left( x \right)\forall x\in {{D}_{f}}\And \text{ }{{D}_{g}}$

For example f(x) = x & g(x) = $\frac{1}{{}^{1}/{}_{x}}$

Solution: f(x) = x is defined for all x

But g(x) = $\frac{1}{{}^{1}/{}_{x}}$ is not defined of x = 0

Hence it is identical for $x ~\in R\text{ }\text{ }\left\{ 0 \right\}$

Quadratic Function

All functions in the form of y = ax² + bx + c where a, b, $c\in R$ , a ≠ 0 will be known as Quadratic function. The graph will be parabolic.

Quadratic Function Domain and Range

At $x=\frac{-b \pm \sqrt{D}}{2}$ , we will get its maximum on minimum value depends on the leading coefficient and that value will be $\frac{-D}{4a}$ (where D = Discriminant)

In simpler terms,

A Quadratic polynomial function is a second degree polynomial and it can be expressed as;

F(x) = ax² + bx + c, and a is not equal to zero.

Where a, b, c are constant and x is a variable.

Example, f(x) = 2x² + x – 1 at x = 2

If x = 2, f(2) = 2.2² + 2 – 1 = 9

Quadratic Function

For Example: y = x² + 1

Read More: Quadratic Function Formula

Rational Function

These are the real functions of the type $\frac{f(a)}{g(a)}$ where f (a) and g (a) are polynomial functions of a defined in a domain, where g(a) ≠ 0.

For example f : P – {– 6} → P defined by f (a) = $\frac{f(a+1)}{g(a+2)}$ , $\forall a\epsilon$ P – {–6 }is a rational function.
Graph type: Asymptotes (the curves touching the axes lines).

Algebraic Functions

A function that consists of a finite number of terms involving powers and roots of independent variable x and fundamental operations such as addition, subtraction, multiplication, and division is known as an algebraic equation.

For Example,

$f(x)=5x^{3}-2x^{2}+3x+6$ , $g(x)=\frac{\sqrt{3x+4}}{(x-1)^{2}}$ .

Cubic Function

A cubic polynomial function is a polynomial of degree three and can be expressed as;

F(x) = ax ³ + bx² + cx + d and a is not equal to zero.

Cubic Function

In other words, any function in the form of f(x) = ax³ + bx² + cx + d, where a, b, c, $d\in R$ & a ≠ 0

Cubic Function Example 1

For example: y = x³

Domain $\in$ R

Range $\in$ R

Modulus Function

The real function f : P → P defined by f (a) = $f(a)=\left | a \right |$ = a, a $\geq$ 0, and f(a) = -a if a<0

\forall a\epsilon

P is called the modulus function.

Domain of f = P
Range of f = $P^{+}\cup {0}$

y=|x|=\left\{\begin{matrix} x & x\geq 0\\ -x & x<0 \end{matrix}\right.

Domain: R

Range: [0, $\infty$ )

Signum Function

The real function f : P → P defined by

\left\{\begin{matrix}\frac{\left | f(a) \right |}{f(a)}, a\neq 0 \\ 0, a=0 \end{matrix}\right.

\left\{\begin{matrix} 1,if x>0\\ 0, if x=0\\ -1, if x<0\end{matrix}\right.

is called the signum function or sign function.(gives the sign of real number)

Domain of f = P,
Range of f = {1, 0, – 1}

For example: signum (100) = 1

signum (log 1) = 0

signum (x²1) =1

Greatest Integer Function

The real function f : P → P defined by f (a) = [a], a $\epsilon$ P assumes the value of the greatest integer less than or equal to a, is called the greatest integer function.

Thus f (a) = [a] = – 1 for – 1 ⩽ a < 0
f (a) = [a] = 0 for 0 ⩽ a < 1
[a] = 1 for 1 ⩽ a < 2
[a] = 2 for 2 ⩽ a < 3 and so on…

The greatest integer function always gives integral output. The Greatest integral value that has been taken by the input will be the output.

For example: [4.5] = 4

[6.99] = 6 [1.2] = 2

Domain $\in$ R

Range $\in$ Integers

Fractional Part Function

Fractional part function {x} = x – [x]

It always give fractional value as output.

For example:- {4.5} = 4.5 – [4.5]

= 4.5 – 4 = 0.5

{6.99} = 6.99 – [6.99]

= 6.99 – 6 = 0.99

{7} = 7 – [7] = 7 –7 = 0

Even and Odd Function

If f(x) = f(-x) then the function will be even function & f(x) = -f(-x) then the function will be odd function

Example 1:

f(x) = x²sinx

f(-x) = -x²sinx

Here, f(x) = -f(-x)

it is odd function.

Example 2:

f(x)={{x}^{2}}

and $f(-x)={{x}^{2}}$

f(x)=f(-x)

It is an even function.

Periodic Function

A function is said to be a periodic function if there exist a positive real numbers T such that f(u – t) = f(x) for all x ε Domain.

For example f(x) = sinx

f(x + 2π) = sin (x + 2π) = sinx fundamental

then period of sinx is 2π

Composite Function

Let A, B, C be three non-empty sets

Let f: A B & g : G C be two functions then gof : A C. This function is called composition of f and g

given g of (x) = g(f(x))

For example f(x) = x² & g(x) = 2x

f(g(x)) = f(2x) = (2x)² = 4x²

g(f(x)) = g(x²) = 2x²

Constant Function

The function f : P → P defined by b = f (x) = D, a $\epsilon$ P, where D is a constant $\epsilon$ P, is a constant function.

Domain of f = P
Range of f = {D}
Graph type: A straight line which is parallel to the x-axis.

In simple words, the polynomial of 0th degree where f(x) = f(0) = $a_{0}$ =c. Regardless of the input, the output always results in constant value. The graph for this is a horizontal line.

Constant Function

Identity Function

P= set of real numbers

The function f : P → P defined by b = f (a) = a for each a $\epsilon$ P is called the identity function.

Domain of f = P
Range of f = P
Graph type: A straight line passing through the origin.

Functions Video

Domain, Range, Period of Functions

Functions and Relations